2017-12-26 | 分类技术随笔 | 标签 CAT

前言

最近翻译技术课的内容是机器翻译。一种机器翻译方法是基于实例的机器翻译方法（EBMT）。比如有这样一对原文和译文：I love apples->我爱苹果。那么基于这个例子，可以把I love oranges翻译为我爱橘子。它需要双语语料，词典和其它分词、句法、语义等分析工具辅助。

计算机辅助翻译软件中用到的翻译记忆就提供了句对齐的双语语料，但目前的CAT软件中只有国产的雪人CAT应用了EBMT技术。雪人CAT界面简洁、功能强大，一直是我的主要CAT软件。最近想参考雪人CAT的功能再自己实现一款CAT软件。

而翻译记忆和EBMT的一个基础就是比较文本的相似度并算出具体差异。这时一般使用的是编辑距离算法。

什么是编辑距离

引用互动百科：编辑距离，又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

如何计算

对于算法的原理我其实也是一知半解，尽量把我理解的讲清楚吧。

首先是维基上的这张公式：

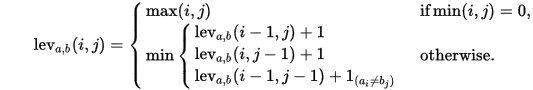
这是使用了一个递归的方法。维基里讲的不清楚，我在quora上看了一些例子后明白了很多。递归的方法就是把算两个文本的编辑距离这一问题分解成了很多的小问题。公式中的lev(i-1,j)是删除操作，lev(i,j-1)是增加操作，而lev(i-1,j-1)说明两个文本相同或需要进行替换。

具体的例子，比如说算sitting和kitten的编辑距离，第一步，根据公式，要进行以下三个部分的计算，并取最小值：

这里x是sitting的长度，为7，y是kitten的长度，为6。cost是公式中后面的+1，如果对应的是公式中的第三条（lev(x-1,y-1)）且末尾字母相同则+0.

lev(x, y)（sitting和kitten）算下去：

lev(x-1, y): 对应sittin和kitten，编辑距离是2 cost=1

lev(x, y-1): 对应sitting和kitte，编辑距离是4 cost=1

lev(x-1, y-1): 对应sittin和kitte，编辑距离是3 cost=1

对应第一条公式，删除g

取最小值lev(x-1, y)+1=3，因此编辑距离是3。以上的编辑距离是我自己算的，实际计算还要进一步计算。下面是完整的过程。

lev(x-1, y)（sittin和kitten）算下去：

lev(x-2, y)：对应sitti和kitten 编辑距离是3 cost=1

lev(x-1, y-1)：对应sittin和kitte 编辑距离是3 cost=1

lev(x-2, y-1)：对应sitti和kitte 编辑距离是2 （末位字母相同）cost=0

对应第三条公式，末位相同，不需操作

lev(x-2, y-1)（sitti和kitte）算下去：

lev(x-3, y-1)：对应sitt和kitte 编辑距离是2 cost=1

lev(x-2, y-2)：对应sitti和kitt 编辑距离是2 cost=1

lev(x-3, y-2)：对应sitt和kitt 编辑距离是1 cost=1

对应第三条公式，末位不同，进行替换

lev(x-3, y-2)（sitt和kitt）算下去

lev(x-4, y-2)：对应sit和kitt 编辑距离是2 cost=1

lev(x-3, y-3)：对应sitt和kit 编辑距离是2 cost=1

lev(x-4, y-3)：对应sit和kit 编辑距离是1 （末位字母相同）cost=0

对应第三条公式，末位相同，不需操作

lev(x-4, y-3)（sit和kit）算下去：

lev(x-5, y-3)：对应si和kit 编辑距离是2 cost=1

lev(x-4, y-4)：对应sit和ki 编辑距离是2 cost=1

lev(x-5, y-4)：对应si和ki 编辑距离是1 （末位字母相同）

对应第三条公式，末位相同，不需操作

lev(x-5, y-4)（si和ki）算下去：

lev(x-6, y-4)：对应s和ki 编辑距离是2 cost=1

lev(x-5, y-5)：对应si和k 编辑距离是2 cost=1

lev(x-6, y-5)：对应s和k 编辑距离是1 cost=1

对应第三条公式，末位相同，不需操作

lev(x-6, y-5)（s和k) 算下去：

lev(x-7, y-5)，x-7=0，停止运算，返回y-5=1

lev(x-6, y-6)：y-6=0，停止运算，返回x-6=1

lev(x-7, y-6)：两者都为0，停止运算，返回0。

对应第三条公式，末位不同，需要替换

通过以上7步运算，对编辑距离的原理应该比较清楚了。

这个递归算法的一个缺点就是会重复运算很多编辑距离。于是维基上的一个优化方法是使用矩阵来保存计算的结果，类似于动态规划的方法。动态规划比较难懂，我这里就不具体讲了。

最后得到这样一个矩阵

		k	i	t	t	e	n
	0	1	2	3	4	5	6
s	1	1	2	3	4	5	6
i	2	2	1	2	3	4	5
t	3	3	2	1	2	3	4
t	4	4	3	2	1	2	3
i	5	5	4	3	2	2	3
n	6	6	5	4	3	3	2
g	7	7	6	5	4	4	3

其中的a(i,j)的值对应公式，是a(i-1,j)+1, a(i,j-1), a(i-1,j-1)+temp三者中的最小值。根据生成的矩阵，我们可以回溯出进行了哪些操作。回溯从右下角开始，比较上方，左方和斜上方的数字。如果数值相同，优先级是斜上、左和上。上表示添加，下则表示删除，斜上则表示替换或相同。另外如果左上，上边，都没有值，只能比较左边的值了。

和翻译记忆结合来说明的话，其中替换和删除操作的部分就是要翻的原文中多出来的，而增加的部分是翻译记忆原文中多出来的。

以下是我用B4J写的一个显示文本差异的小程序。